ABSTRACT
A traditional method of controlling evaporator superheat in a vapor compression air conditioning system is the thermostatic expansion valve (TXV).  Such systems are often used in automotive applications.  The TXV depends on superheat to adjust the valve opening.  Unfortunately, any amount of superheat causes that evaporator to operate at reduced capacity due to dramatically lower heat transfer coefficients in the superheated region.  In addition, oil circulation back to the compressor is impeded.  The cold lubricant almost devoid of dissolved refrigerant is quite viscous and clings to the evaporator walls.  A system that could control an air conditioner to operate with no superheat would either decrease the size of its existing evaporator while maintaining the same capacity, or potentially increase its capacity with its original evaporator.  Also, oil circulation back to the compressor would be improved.  To operate at this two-phase evaporator exit condition a feedback sensor would have to quantify the quality of liquid mass fraction (when the exit stream is a mixture of droplets and superheated vapor) of the refrigerant exiting the evaporator.

INTRODUCTION
One of the most common control schemes for a vapor compression air conditioning system is the use of a thermostatic expansion valve (TXV).  TXV systems use a remote thermal bulb at the exit of the evaporator.  This bulb causes the TXV to open and close in response to changes in superheat of the refrigerant at the evaporator outlet.  If the temperature of the refrigerant increases rapidly, as would be the case when the heat load was suddenly increased, the power element would open the valve and admit more liquid refrigerant to the evaporator.  Once in the evaporator, the liquid refrigerant absorbs heat by changing state from liquid to gas.  By the time it leaves the evaporator, the gaseous refrigerant has been superheated a few degrees.

By allowing the evaporator to operate with some finite superheat at its exit, some portion of the evaporator will have only vapor flowing through it (no liquid).  This situation decreases the refrigerant-side heat transfer.  This portion of the evaporator is not able to vaporize refrigerant, and is only able to transfer heat via the sensible heating of the refrigerant.  This process can reduce the capacity of the evaporator.

Any control scheme that uses superheat as its control signal (e.g. TXV systems) must have some finite superheat.  Such a system is unable to control the plant to operate in a regime of saturated liquid/vapor at the exit of the evaporator.  The minimum amount of superheat that such a system can use and maintain stability is dependent on the method of measuring the superheat.
The difficulty of a temperature measurement is in part due to the non-equilibrium flow of refrigerant as it exits the evaporator only slightly superheated.  The flow is said to be non-equilibrium because saturated liquid droplets are entrained in superheated vapor. There is just not enough time for the liquid to vaporize and reach equilibrium.  This phenomenon can be attributed to maldistribution of liquid/vapor refrigerant throughout the evaporator and to the nature of two-phase flow [1,2,3,4].  The saturated liquid droplets in superheated vapor flow regime cause temperature transducers to exhibit large variances.
In evaporators with imperfect distribution exit streams could be a mixture of superheated vapor and droplets.  Some channels or circuits that are thermally overloaded have superheated vapor at the exit, while others where thermal loads are not sufficient to evaporate all liquid that enters will have some droplets at the exit.  The mixture of these streams is in thermal non-equilibrium.  After sufficient time (or length of pipe) droplets could completely evaporate, reducing superheat.  But if the sensible heat available in the superheated vapor is not enough energy to vaporize all droplets, then the exit is in the quality region.  Liquid-mass-fraction (LMF), which is the mass of liquid in vapor of any state, is one parameter to describe the state at the evaporator exit, as described in Shannon, Hrnjak, and Leicht [12].

A temperature transducer measuring the temperature of refrigerant in this non-equilibrium flow regime can read the saturation temperature (if a liquid droplet is on the transducer), or can read the temperature of the superheated vapor (which may not be constant), or can read any value in between.  A large variance in a control signal (e.g. superheat) can cause a controller to hunt.  Since the non-equilibrium flow has superheated vapor along with liquid droplets, quality cannot be used to correctly describe the state of the refrigerant.

Some of the best TXV systems are only able to maintain stable operation with a minimum of about 5 degrees Fahrenheit.  But, a patent does exist for a transducer that appears to function in a similar fashion as the device described in this paper.  Patent number 2219661 was granted on May 13th, 1992 to York International Ltd by the Comptroller-General of Patents, Designs and Trade Marks, United Kingdom Patent Office.  In addition several companies are currently pursuing a prototype commercial transducer.  However to the authors’ knowledge no results for this class of sensors has appeared in the open literature.

THE SENSOR
A sensor that could estimate the liquid mass fraction (LMF) at the exit of the evaporator could be used in the feedback loop of a control scheme that would maintain the refrigerant at a constant LMF. Liquid mass fraction (LMF) is the ratio of the mass of liquid to the total mass of the fluid, whether or not it is in equilibrium.

PREVIOUS WORK
One of the early studies of superheat stability was carried out at the University of Illinois by Wedekind and Stoeker in the 1970’s [1, 2, 3].  The project addressed the stability of the location of the last evaporated droplet in a straight, electrically heated, glass tube. It was found that the location of the last evaporated droplet (the end of the two-phase region) is a stochastic function and the distribution was determined.  Some years ago Barnhart and Peters studied stability at the exit of a single glass tube serpentine evaporator [4].  They observed the same phenomena described by Stoecker and determined that most of the instabilities at the exit were generated far upstream (also see [13]).

In another project the unsteadiness of the exit temperature signal was used as an identifier of “stable” operation [12].  The idea of using the variance of the temperature signal at the exit of the evaporator for better flow was developed.
That idea was further developed in a project whose objective was to develop a micro electromechanical system (MEMS) sensor that would do a better job of sensing droplets at the evaporator exit than a thermocouple.  A new MEMS sensor (a heated resistance temperature detector RTD) was developed.

The MEMS RTD was driven by a current source and the voltage drop across the sensor was the measured variable (see Figure 1). This voltage is a function of the temperature of the sensor. Notice that this device is essentially an uncompensated hot film anemometer (see page 90 of [5]). Hot wire anemometers have been used to detect droplets entrained in gases (page 181 of [5]). The sensor is cooled as each droplet strikes the hot sensor and is evaporated.

FUNCTIONALITY OF SENSOR
An interesting variation is the use of constant resistance transducer control. This variation of the circuit tries to keep the resistance of the RTD  equal to Rset . The voltage Vo is then directly proportional to the current needed to achieve this condition. The power removed by heat transfer into the refrigerant stream is, of course, the square of the current flowing through the RTD times the RTD resistance.

This circuit uses an operational amplifier as the medium for feedback.  The op-amp uses the feedback to maintain its inputs at constant voltage while drawing very little current.  This is what forces the resistance of the RTD to be equal to the resistance of Rset.  Traditionally, an RTD is used to measure temperature by measuring the resistance of the RTD as it changes with temperature.  But, this circuit forces the resistance of the RTD to be equal to Rset.  The circuit compensates by heating up the RTD until the resistance (and thus the temperature) of the RTD is equal to Rset.

Such a system has a much wider bandwidth (that is, it will respond to much higher rate variations in heat flux). The reason is as follows. Constant current excitation requires that the transducer temperature changes for any change in transducer resistance and hence signal to be observed. This is an inherently slow (relatively long time constant) process dominated by the thermal capacity of the transducer body. Constant resistance operation implies that the circuitry varies the transducer current so that the transducer stays at a constant resistance and hence a constant temperature. The thermal energy stored in the transducer body does not change. This technique is used with hot wire anemometers and provides very broadband performance (bandwidths up to 0.5 MHz). The technique also has the advantage of protecting the sensor from overheating.

The circuit maintains the voltage drop across the RTD equal to half of V0.  And since the Rset is equal to the resistance of the RTD, the power dissipated through the RTD can be determined.  By measuring the temperature of the refrigerant passing over the sensor and inferring the temperature at the surface of the RTD from Rset, the difference of these temperatures can be found.  This paper refers to this temperature difference as overheat. The overheat represents the driving potential that allows power to be dissipated through the sensor.

The ratio of the power dissipated to this temperature difference can be interpreted as "the surface-to-free-stream thermal conductance" between the RTD and refrigerant.  It is essentially the convection heat transfer coefficient multiplied by the effective surface area (hA).  This surface-to-free-stream thermal conductance (hA) does not depend on the effective surface area of the sensor because neither the geometry nor the orientation of the sensor varies.  This hA parameter is particularly sensitive in the high quality/low superheat region (low LMF).  As the LMF of a fluid increases, so does its hA.
As a droplet of saturated liquid refrigerant clings to the surface of the RTD, the RTD circuitry will do what it can to raise its temperature back its set point (which is determined by Rset).  To do this the RTD must transfer enough energy to the refrigerant to overcome its latent heat of vaporization.  As the LMF of the fluid decreases, less energy is dissipated through the RTD.  When the fluid becomes all vapor, all of the energy flux through the RTD goes to sensible heat that is needed to raise the temperature of the RTD to its set point.

DATA COLLECTION
In order for the sensor to be useful some relationship between refrigerant quality, overheat (temperature difference), and power dissipated through the sensor needs to be developed.  Quality is determined from the enthalpy of the refrigerant entering the calorimeter.  Overheat is the difference between the temperature of the RTD and the temperature of the refrigerant.  The power dissipated through the RTD is determined by the square of the RTD’s voltage drop divided by its resistance.
Experiments were conducted that would demonstrate the dependence of sensor power and overheat while the quality was held constant.  Figure 4 shows the results of such experiments.  The results show that power dissipated is a linear function of overheat (the temperature difference between the sensor and the refrigerant).  The data agrees with the convection heat transfer model which takes the form:

Ts is the fixed temperature at the surface of the RTD.  Tinf is the temperature of the free-stream refrigerant passing over the sensor.  The power dissipated can be modeled as the energy transfer q.  The overheat in the system is analogous to (Ts - Tinf).  And the slope of the line represents hA.  hA is the product of the convection heat transfer coefficient and the effective surface area.

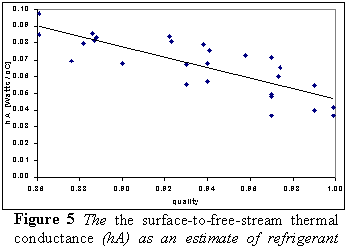
Once it was established that hA is constant for a given quality, the next task was to develop a relationship between quality and hA.  Figure 5 shows the results of an experiment where the RTD sensor was subjected to various qualities.  Quality was measured by using a calorimeter in the method described earlier.

As quality decreases more and more liquid droplets hit the sensor.  This demands more power to be dissipated through the sensor in order for the sensor to maintain its constant temperature.  At the same time the temperature of the refrigerant is fixed at its saturation temperature.  So the ratio of the dissipated power to the overheat (hA) increases as quality decreases.  This theory is supported by the data shown in figure 5.

One reason for the significant scatter in the data may be due to the inaccuracies in measuring quality.  Quality at the exit of the evaporator was inferred indirectly.  What was actually estimated was the quality of refrigerant entering the calorimeter after it had passed through a mixer.  Implicit to the data used to construct figure 5 are the assumptions that the refrigerant passing over the sensor was saturated liquid/vapor and that none of the refrigerant changed phase between the sensor and the entrance of the calorimeter.  Neither one of theses assumptions is necessarily true.
 
 

EXPERIMENTAL RESULTS

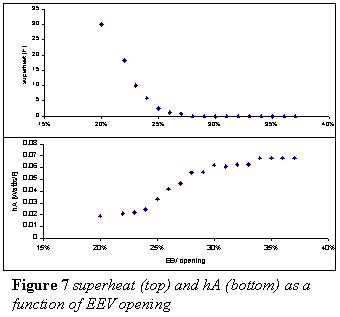
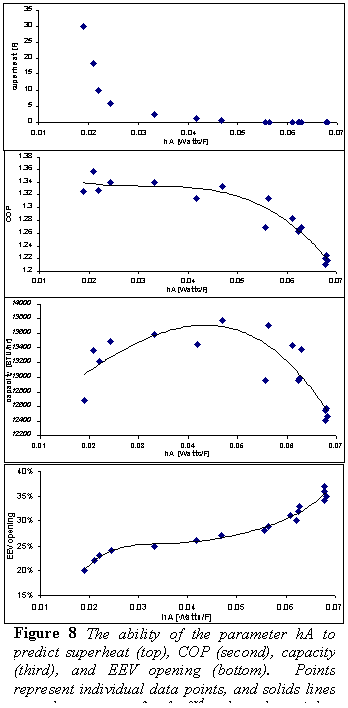
Figure 8 demonstrates the sensor’s ability to predict system performance.  COP is relatively flat over regions of high superheat (low hA).  It does not significantly drop off until well into the two-phase region (no superheat and high hA).  According to this data, the capacity peaks out somewhere around 0.04 and 0.05 Watts/oF.  This is the region where the system has its maximum cooling power for the set of operation conditions.  This region corresponds to little to no superheat.

Capacity measurements are taken from the difference in enthalpies between the air going into the evaporator and the air coming out.  Volumetric flow rates are measured using a venturi on the air loop on the evaporator side.  Relative humidity and temperature measurements are taken for the air going in and coming out of the evaporator.
 
 

Figure 8 also suggests that COP is not significantly compromised at the point were capacity seems to reach its maximum.

REFERENCES
1. Wedekind, G. L., Stoecker W. F., (1966), Transient Response of the Mixture - Vapor Transition Point in Horizontal Evaporation Flow, ASHRAE Transactions, Vol. 72, Part II.

2. Stoecker, W. F., (1966), Stability of and Evaporator-Expansion Valve Control Loop, ASHRAE Transactions, Vol. 72, Part II.

3. Wedekind, G. L., (1965), Transient response of the mixture -vapor transition point in two-phase horizontal evaporating flow, Ph.D.

4. Barnhart, J.S., Peters, J.E., (1992): An Experimental Investigation of Flow Patterns and Liquid Entrainment in a Horizontal -Tube Evaporator, ACRC Technical Report #28, December, 234 pp.

5. Lomas, C. G., (1986), Fundamentals of Hot Wire Anemometry, Cambridge University Press.

6. Collins, C.D., N.R. Miller, and W.E. Dunn.  Experimental Study of Mobile Air Conditioning System Transient Behavior.  ACRC Technical Report 102, July 1996.

7. Rubio-Quero, J.E., W.E. Dunn, and N.R. Miller. A Facility for Transient Testing of Mobile Air Conditioning Systems,  ACRC Technical Report 80, June 1995.

8. Weston, P.G., W.E. Dunn, and N.R. Miller. Design and Construction of a Mobile Air-Conditioning Test Facility for Transient Studies, ACRC Technical Report 97, May 1996.

9. Wandell, E.W., W.E. Dunn, and N.R. Miller.  Experimental Investigation of Mobile Air Conditioning System Control for Improved Reliability, ACRC Technical Report 128, August 1997.

10. Miller, James A. (1976) A Simple Linearized Hot-Wire Anemometer, Journal of Fluids Engineering, December 1976.

11. Simpson, R. L., K. W. Heizer, R. E. Nasburg. Performance Characteristics of a Simple Linearized Hot-Wire Anemometer, Journal of Fluids Engineering, September 1979.

12. Shannon, M. A., P. S. Hrnjak, T. M. Leicht. Exploratory Research on MEMS Thechnology for Air Conditioning and Heat Pumps  EPRI Report TR-1111699
 

last modified 1 august 2000                         send problems and queries to webmaster at:  jamessolberg@hotmail.com