The Dynamics of the Pole Vault
 
 
 

introduction   |  initial model   |   simulation   |   final model   |  conclusion



Introduction
Pole vault is an event in track and field where an athlete’s task is to get his entire body over a cross-bar without knocking it off, and using only a single pole and his body.  All of the energy used by the vaulter to clear the cross-bar must come from the athlete.  The vaulter makes use of the runway to obtain his maximum velocity before take off.  From the vaulter’s velocity at take off, his mass has an initial kinetic energy associated with it.  Although, most of the energy in the system is due to the vaulter’s initial kinetic energy, the vaulter’s muscles are able to put additional energy into the system once he has left the ground.

Initial Model
The initial model only factors in the kinetic energy of the approach of the vaulter.  Using this model, the following assumptions are made:
1. The only energy put into the system is the kinetic energy of the vaulter’s mass.
2. Maximum height is obtained when his kinetic energy is equal to zero (a point of instantaneous zero velocity).
3. No loss of mechanical energy (all kinetic energy is converted directly to potential energy).
4. No energy losses in the pole (perfect elastic member).
5. No energy losses between the vaulter’s take-off foot and the ground.

Using a simple energy balance of kinetic and potential energy, and following the assumptions, the maximum height of the vaulter is given by h = v2/(2*g); where h is the maximum height, v is the velocity of the vaulter at take off and g is the acceleration due to gravity (9.81 m/s2).  If all of my assumptions were valid, then the maximum height of a vaulter is only a function of the square of his velocity.  Also, for a given vaulter’s maximum velocity he could only obtain the following height:


 
velocity (m/s)
CGinitial height (m)
CG final height (m)
CG final height (ft.)
6
1
2.835
9.298
7
1
3.497
11.472
7.5
1
3.867
12.684
8
1
4.262
13.979
8.5
1
4.682
15.358
9
1
5.128
16.821
9.5
1
5.600
18.368
10
1
6.097
19.998
10.25
1
6.355
20.844
10.5
1
6.619
21.711
Table I. Idealized maximum heights for a given take-off velocity, given the assumptions stated.  His initial height of his center of gravity is due to the fact that his center of gravity starts out at a meter above the ground at take-off.
The fastest 100m dash ever recorded was done in 9.84 seconds; which gives an average speed of 10.16 m/s.  The sprinter had to, of course, run faster than 10.16 m/s at one point, due to the fact that he initially started at zero.  The top speed of any human (under only his own power) is estimated at 10.5 m/s.  This velocity corresponds to a 21.7 foot jump.  But the world record is only 20.2 feet.  Due to running mechanics of a pole vaulter (while carrying the pole),  it is estimated that a vaulter could probably only obtain speeds of about 9.5 m/s at take-off.  But this velocity corresponds to a maximum height of only 18.4 feet (significantly less than the world record).  A better method of analysis is needed.


 
Simulation
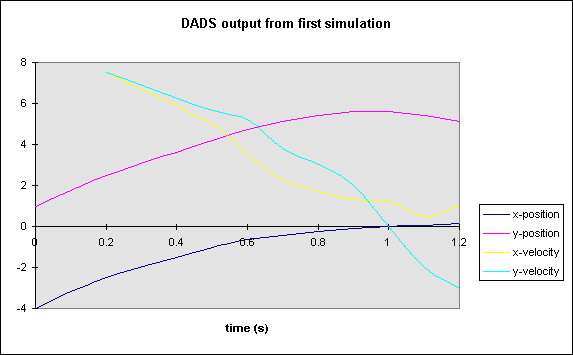
Closed formed solutions for all torques and displacements are nice to have, but they are often tedious and impractical (as in this case).  Simulation software packages are available to calculate these parameters using numerical methods.  DADS (Dynamic Analysis and Design System) is one such package.  The first model that I simulated on DADS is identical to that I analyzed using the Lagrangian method.  An initial velocity of 9.5 m/s was given to the vaulter.  Graph I shows the data collected from the simulation.
graph I.  Data collected from DADS first simulation.
As you can see from graph I, his maximum height is somewhere around 5.5 m.  This is comparable to our calculated value (Table I) of 5.6 m , when his initial velocity was 9.5 m/s.

Final Model
In my initial model I made many assumptions to simplify my model.  In reality, some of these assumptions are not good approximations.  Assumption 5 (No energy losses between the vaulter’s take-off foot and the ground.) is a pretty poor assumption.  Ideally, the vaulter would like to take off at 45 degrees from the horizontal.  That would mean that within one step, the vaulter would change his momentum from going totally horizontal to an angle of 45 degrees to the horizontal.  This is a tremendous impulse on the foot ( about 700 kg*m/s).  In reality take off angle is somewhere around 20 degrees to the horizontal.  Even then the impulse is quite large and energy is lost (the vaulter will slow down at take off) due to this effect.

Assumptions 3 and 4 are actually quite accurate (No loss of mechanical energy (all kinetic energy is converted directly to potential energy).  and  No energy losses in the pole (perfect elastic member).).  The efficiency of the pole is probably at least 95%.

Assumption 2  (Maximum height is obtained when his kinetic energy is equal to zero (a point of instantaneous zero velocity)) is not exactly accurate.  The vaulter needs some horizontal component of velocity to go over the crossbar (so he does not fall on it).  But the velocity is usually small (about 2 m/s), and since kinetic energy is proportional to the square of the velocity, his kinetic energy at maximum height is less than 5% of his total energy.

So far all of the assumptions seem to help the theoretical vaulter (he can jump higher with these assumptions).  But yet our calculated maximum height is significantly less than the world record.   The additional height is gained when assumption 1 is no longer used (The only energy put into the system is the kinetic energy of the vaulter’s mass.).

The final model allows energy to be put into the system after the vaulter has left the ground.  The additional energy is provided by his shoulders.  His shoulders provide an input torque that:  raises his center of gravity by some additional amount, and creates some additional rotational kinetic energy.

For the final model the pole was divided into 5 equal sections and given 4 rotational springs.  Also, the body of the vaulter is modeled as a six-bar linkage.  The six bars are
· top link of the pole
· right fore arm
· left fore arm
· right upper arm
· left upper arm
· mass of the vaulter

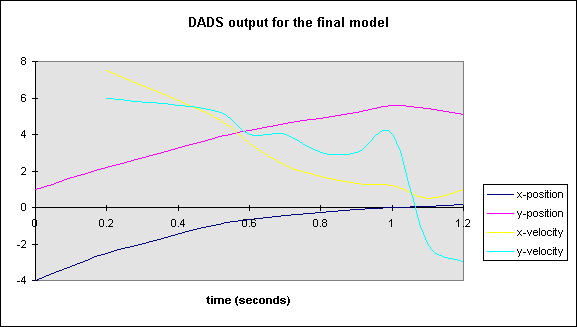
The DADS simulation was set up similar to before with the following results in graph II.

Graph II.  DADS output for the final model.
Graph II shows his maximum height at about 5.5 meters (t = 1 second).  But he also has a vertical component of velocity equal to about 4 m/s.  If all of the kinetic energy at this point was converted into potential energy to raise his center of gravity an additional amount, he would go an addition v2 / (2*g) = 0.82 meters.  So, his final height would be about 6.3 meters, which is 20.7 feet which is about a half of a foot higher than the world record.

Conclusion
The maximum height that a pole vaulter can obtain is heavily depends on his initial velocity.  This is where he gets most of his energy.  But, once he takes off of the ground it is possible for him to put some additional energy into the pole.  Theoretically, if a vaulter is able to take off from the ground at 9.5 m/s, and able to supply additional energy efficiently to the pole, he could jump 20.7 (20’ 8 1/2 ‘’).

introduction   |  initial model   |   simulation   |   final model   |  conclusion

TOP OF PAGE   |   BACK to engineering credentials   |   BACK to engineering projects   |   JAMES' HOME

last modified 1 august 2000