Introduction
This project is an extension of the research conducted for my Master of Science.  The reader should be familiar with Regulation of the Liquid Mass Fraction of the Refrigerant Exiting an Evaporator before proceeding.  That project presented a method for estimating the liquid-mass fraction (LMF) of the refrigerant exiting the evaporator.  The assumptions used in that analysis violated some fundamental engineering doctrines.  While that crude method of data reduction was able to stably control the expansion valve, the system was not nearly generic enough to be applied to an arbitrary air conditioning or refrigeration system.
This project will develop and implement a neural network capable of more accurately predicting the LMF of refrigerant.  The output of the neural network will be the actual LMF (as opposed to a control signal that could inferred as a function of the LMF)

The previous model reduced three parameters (temperature of the sensor, temperature of the refrigerant, and the voltage across the sensor) to estimate the LMF.  Three parameters were used because the reduction of data had to be as simple as possible.  But, the use of neural networks allows an arbitrary number (within reason) of parameters, each of which have arbitrary relations to each other and to the output.  Initially, every recorded variable that influenced the LMF of the refrigerant was used in the analysis.  These included:

Tsensor [oC].  (The temperature of the sensor)  This was inferred from the resistance of the sensor.  The resistance of the sensor is known, because it is equal to Rset (see section 1.2.3).  The temperature of an RTD is a linear function of its resistance.

VDC.  (The DC voltage across the sensor)  This is measured by a multimeter on the HP data acquisition system.

VRMS.  (The root-mean square of the voltage of the voltage across the sensor)  The RMS voltage was measured with specific hardware on the data acquisition system, but could have been estimated using equation 1.2 (refer to section 1.3.3.1).

Tref_out [oC].  (The temperature of the refrigerant coming out of the evaporator)  This is the refrigerant immediately before it passes over the sensor.  This may also be referred to as the “free stream” temperature.

mdot [grams/sec].  (the mass flow rate of the refrigerant)  This is measured by a MicromotionTM Coriolis flow meter.

Pevap [kPa].  (the absolute pressure in the evaporator)  This pressured is assumed to be same as the pressure of the refrigerant flowing over the sensor.

Tref_in [oC].  (the temperature of the refrigerant going into the evaporator)

Tmix [oC].  (The temperature of the refrigerant after it has passed over the sensor and has been well mixed)  The refrigerant passing over the sensor is not in thermal equilibrium.  As a result the reading from the temperature sensor (thermocouple) may not be accurate, because it is not known what it being read (the temperature of the possibly superheated vapor, or the temperature of the saturated liquid?).  Tmix is in thermal equilibrium, and is a more stable measurement.

dPevap [dkPa].  (differential pressure across the evaporator)  The pressure drop across the evaporator is an indication of the velocity of the refrigerant.

Pmix [kPa].  (pressure of the refrigerant after it has passed over the sensor and come to thermal equilibrium)

The output of the neural network is:
LMF.  (liquid-mass-fraction of the refrigerant exiting the evaporator) Liquid-mass-fraction (LMF), which is the mass of liquid in vapor of any state, is a measure to describe the state at the evaporator exit, as described in Shannon, Hrnjak, and Leicht
 

2.7 Reduction of Inputs
A sensitivity analysis on the inputs to a neural network indicates which input variables are considered most important by that particular neural network.  Sensitivity analysis can give important insights into the usefulness of individual variables.  It often identifies variables that can be safely ignored in subsequent analysis, and key variables that must always be retained.  However, it must be deployed with some care, for reasons that are explained below.

Input variables are not, in general, independent – that is, there are interdependencies between variables.  Sensitivity analysis rates variables according to the deterioration in modeling performance that occurs if that variable is no longer available to the model.  In so doing, it assigns a single rating value to each variable.  However, the interdependence between variables means that no scheme of single ratings per variable can ever reflect the subtlety of the true situation.  There may be interdependent variables that are useful only if included as a set.  If the entire set is included in a model, they may be accorded significant sensitivity, but this does not reveal the interdependency.  Worse, if only part of the interdependent set is included, the sensitivity of the others will be zero, as they carry no important information.

Sensitivity analysis does not rate the "usefulness" of variables in modelling in a reliable or absolute manner.  You must be cautious in the conclusions you draw about the importance of variables.  Nonetheless, in practice it is extremely useful.  If a number of models are studied, it is often possible to identify key variables that are always of high sensitivity, others that are always of low sensitivity, and "ambiguous" variables that change ratings and probably carry mutually redundant information.

A datasheet was constructed to estimate the importance of each variable. It indicates the sensitivity of each variable.  Sensitivity is reported separately for training and verification subsets – the consistency of the sensitivity ratings across the two subsets is a good initial cross check on the reliability of the sensitivity analysis.  The sensitivity is reported in three rows – the Rank, Error, and Ratio.  The basic sensitivity figure is the Error.  This indicates the performance of the network if that variable is "unavailable."  Important variables have a high error, indicating that the network performance deteriorates badly if they are not present.  The Ratio reports the ratio between the Error and the Baseline Error (i.e. the error of the network if all variables are "available").  If the Ratio is one or lower, then making the variable "unavailable" either has no effect on the performance of the network, or actually enhances it!  The Rank simply lists the variables in order of importance (i.e. order of descending Error), and is provided for convenience in interpreting the sensitivities.

The average over the four trials presented in this experiment:
 

     1.Tsensor

2.8 Determining the Number of Hidden Layers

Selecting the number of hidden units in a neural network is in principle no different from selecting regressors in a linear regression or the order of a polynomial regression.The main ideas that have been developed in that field are pruning by small steps (backward selection), incremental construction (forward selection), and minimizing some measure of performance over the class of possible models.

All the routines aim to predict the performance on a test set, and so to select the model with the best performance on the test set.The most general idea is to use cross-validation for neural nets.How do we move from the whole set to a subset for training?Do we start at the fitted weights for the whole data?This could bias the procedure.If we start at another random starting point, we could end up at a very different solution even with the whole data, let alone with a subset.This shows that the learning procedure for a neural network is not well defined, as there are often multiple local minima of rather different performance.

Once again our encapsulated software saviour, Statistica Neural Networks, comes to our rescue. Statistica does its best to make to the best decisions for our network, but no known algorithm is able to optimize the network perfectly.But, nonetheless, we trust logic of the software.

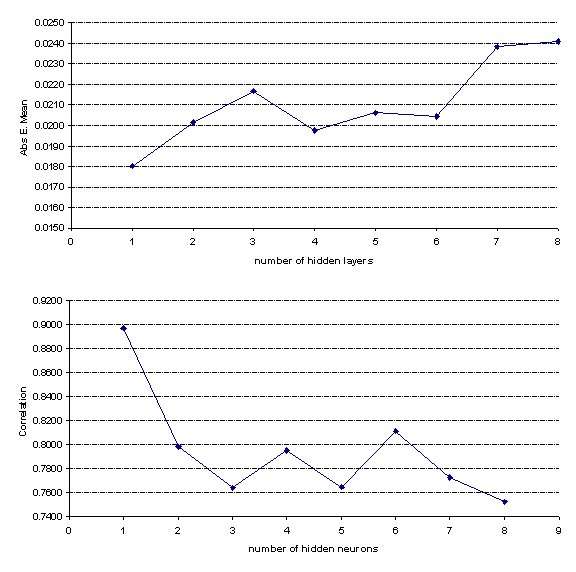
One way to investigate the effect of the number of neurons in the hidden layer is to run a series of networks where the only thing that changes between the networks is the number of hidden neurons.The base network will use seven inputs (see the previous section), 28 cases for testing, 10 for verification, and 12 for testing

To help reduce the data some of the testing regression data was plotted on the same graph for the various numbers of hidden neurons. The test set was used because it is not used in training at all, and is designed to give an independent assessment of the network's performance when an entire network design procedure is completed.The two statistics that were plotted were:

1. Abs. E. Mean.  Average absolute error (difference between target and actual output values) of the output variable.

2. Correlation.  The standard Pearson-R correlation coefficient between the target and actual output values

2.10 Further Simplification

The first variable that I have chosen to discard is Tmix.Tmix is numerically close to Tref_out.Tmix can also usually be determined by knowing what Pmix.It is usually the case that when Tmix is measured that the refrigerant is in a saturated state. Thus, Tmix is a function of Pmix (and vice versa).The regression statistics for the same network but with only six inputs are:

The statistics are very similar, but maybe a bit worse.The abs error mean for the test cases went from 0.019 to 0.020.For all of the networks used in this section the same cases were used for training, verification, and testing.

The next variable to be removed in dPevap.This is an important variable in estimating the speed of the refrigerant flowing over the sensor.Since the sensor actually measures the heat transfer coefficient of its surface, the speed of the refrigerant is an important factor to know.But, we still have the mass flow rate of the refrigerant (mdot).The speed of the refrigerant can be inferred from mdot.The regression statistics for the same network with five inputs (dPevap and Tmix taken out):

Once again the statistics are very similar to those in the previous network.Thus far, removing these two variables has had little effect on the performance of the network.Let’s try to remove only more variable.Pmix is the next logical variable to remove.Pmix was very strongly correlated with the other variables.At this point we should really start to see the performance of the network suffer.The statistics for the network with only four variables are as follows:

The statistics do show that there is a significant degrade in the performance of the network without this variable.At this point the abs error mean for the test cases for this network has actually dropped below the abs error mean for the original model (0.0258).But, the training cases still perform better than the original model.The training cases would actually be a more fair comparison with the original model.  Because with the original model, all of the data points were used to fit a line through the data points.Then those same data points were used to assess the performance of the model.So there is no measure of the original model’s ability to generalize to other cases.

Also, in defense of the neural network model the original model used two separate models for the two different mass flow rates.To do a completely fair comparison between the two types of model, we should construct each model with the same domain of knowledge.Two neural networks will be constructed (one for high mass flow rate and the other for the lower mass flow rate), and the neural networks will only have the inputs that the original model had (Tsensor, VDC, and Tref_in).The networks will have one hidden neuron. The regression statistics for the network for the cases with the lower mass flow rate are:
 
 

	train	verify	test
Data Mean	0.057	0.075	0.052
Data S.D.	0.042	0.051	0.041
Error Mean	0.000	0.000	-0.003
Error S.D.	0.002	0.003	0.006
Abs E. Mean	0.002	0.002	0.004
S.D. Ratio	0.057	0.059	0.148
Correlation	0.998	0.998	0.989

The network performed extremely well.The abs error mean for the test cases was only 0.004.The corresponding abs error mean for the original model (for just the low mdot data) is 0.021; more than five times greater.

A similar network was constructed for the high mass flow rate data.The results went as followed:
 
 

	train	verify	test
Data Mean	0.069	0.087	0.077
Data S.D.	0.058	0.077	0.047
Error Mean	-0.011	0.000	-0.021
Error S.D.	0.026	0.028	0.057
Abs E. Mean	0.022	0.020	0.042
S.D. Ratio	0.441	0.362	1.219
Correlation	0.898	0.933	0.332

This network didn’t perform nearly as well.The abs error mean for the test cases was 0.042.The corresponding abs error mean for the original model (for just the high mdot data) is 0.029.So, the original model actually performed better than the neural network did for the test cases.But, the neural network performed better in the training cases (abs error mean of 0.022).

2.11 Other Types of Networks

     Kohonen network

     ·Linear network

     ·(Bayesian) Probabilistic network

     ·(Bayesian) Regression network

     ·Perceptron

     ·ADALINE

Given the nature of the relationships between the variables and the output, the best type of network to try on this set of data is the linear network.The system of variables has a much more simple nature than was originally thought.Many of these networks work well for complex systems, and others only work for classification problems.

Linear networks have only two layers: an input and output layer, the latter having linear PSP and activation functions.Many problems cannot be solved (or solved well) by linear techniques; however, many others can, and it is poor practice to neglect a simple technique in favor of more complex ones without comparison.You should always train a linear network, as a standard of comparison for the more complex non-linear ones.Linear networks are best trained using the pseudo-inverse technique:this optimizes the last layer in any network, providing it is a linear layer.Pseudo-inverse is fast, and guaranteed to find the optimal solution.You may also use back propagation, quick propagation, or Delta-bar-Delta, to optimize a linear network, if you desire.This is not usually good practice, although occasionally the pseudo-inverse technique suffers from numerical problems, in which case iterative training provides a fall-back position.

The first linear network constructed used all ten of the original inputs.The regression statistics are as follows:

Recall that the MLP network with the same number inputs had the following regression statistics:
 

	train	verify	test
Data Mean	0.067	0.091	0.056
Data S.D.	0.050	0.066	0.045
Error Mean	0.012	0.000	0.012
Error S.D.	0.013	0.020	0.020
Abs E. Mean	0.015	0.015	0.018
S.D. Ratio	0.261	0.308	0.430
Correlation	0.966	0.966	0.903

Note that the linear network performs significantly better than its MLP counter part.

The next linear network constructed used the seven inputs that were found in section 2.7.The regression statistics are as follows:
 

	train	verify	test
Data Mean	0.067	0.091	0.056
Data S.D.	0.050	0.066	0.045
Error Mean	0.000	-0.018	0.002
Error S.D.	0.028	0.030	0.030
Abs E. Mean	0.021	0.023	0.023
S.D. Ratio	0.572	0.461	0.669
Correlation	0.820	0.911	0.807

There was a significant degrade in the performance of the network after the three inputs were removed.The abs error mean of the test cases dropped from 0.013 to 0.023 in the linear networks.But the corresponding MLP networks had no significant change in the abs error mean of the test cases (0.018).

The next linear network that will be looked at will have Tmix input removed.This was the next variable that was pruned earlier.The following are regression statistics for a six input linear network:

There is virtually no change in the performance of the network from removing Tmix.The MLP network still performed better with six inputs (abs error mean of the test cases of 0.020).

The next linear network will remove the dPevap variable.The regression statistics are as follows:

At this point the performance of the network is beginning to drop below acceptable levels, so no more variables will be removed.The corresponding MLP network had a abs error mean of 0.024 for the test cases.

2.13 Improving the Analysis

Linear.The activation level is passed on directly as the output.Used in a variety of network types, including linear networks, and the output layer of radial basis function networks.

Logistic.This is an S-shaped (sigmoid) curve, with output in the range (0,1).The most commonly-used neural network activation function.

Hyperbolic.The hyperbolic tangent function: a sigmoid curve, like the logistic function, except that output lies in the range (-1,+1).Often performs better than the logistic function because of its symmetry.By default, not used in any network types.Ideal for customization of multilayer perceptrons.

Exponential.The negative exponential function.Ideal for use with radial units.The combination of radial PSP function and negative exponential activation function produces units which model a Gaussian (bell-shaped) function centered at the weight vector.The standard deviation of the Gaussian is given by the formula below, where d is the "deviation" of the unit stored in the unit's threshold:

Softmax.Exponential function, with results normalized so that the sum of activations across the layer is 1.0.Used in the output layer of specialized multilayer perceptrons for classification problems, so that the outputs can be interpreted as probabilities of class membership.

Square root.Used to transform the squared distance activation in a Kohonen network to the actual distance as an output.

Sine.Possibly useful if recognizing radially-distributed data; not used by default.

Ramp.A piece-wise linear version of the sigmoid function.Relatively poor training performance, but fast execution.

Step.Outputs either 1.0 or 0.0, depending on whether the PSP value is positive or negative.

One way to possibly improve a network is to artificially inject noise into the system. Adding noise can have similar benefits to shuffling, in allowing the network to escape local minima during training.It can also provide better generalization performance, by preventing the network from overfitting the training data.

There are wide variety of different types of learning algorithms that were not explored at all. Training algorithms are divided into three types.

Initialization algorithms.These are not really training algorithms at all, but methods to initialize weights (usually randomly) prior to training proper.They do not require any training data.

Supervised learning.These algorithms alter weights and/or thresholds, using sets of training cases that include both input and target output values.

Unsupervised learning.Alter weights and/or thresholds using sets of input training cases (output values are not required, and if present are ignored). The unsupervised learning techniques are mainly used to assign weights and thresholds in radial units; the supervised techniques are mainly used to assign weights and thresholds in linear PSP units.

Some network types require a combination of supervised and unsupervised training algorithms; for example, the radial units in a radial basis function network must first be assigned using unsupervised techniques, with the linear units in the output layer being subsequently assigned using supervised techniques.In general, different techniques can be freely combined in training any particular network, although each technique may have restrictions over where it can be used (e.g., the Kohonen algorithm can only be used if the first hidden layer consists of radial units).

ST Neural Networks also features some auxiliary features associated with training.This includes the random initialization of weights, the definition of stopping conditions for the training algorithms (in particular, training can be stopped once the error performance of the network begins to deteriorate) and the retention of the best network discovered during an iterative training run.

More could have been done with dimensionality reduction.  The only systematic forms of dimensionality reduction that were looked at in detail were sensitivity analysis and reduction by using the correlation matrix.  But, we could have searched based on network performance using genetic algorithm, forward stepwise selection, or backward stepwise selection.  By creating a pre-processing network the effective dimensions on the inputs could have been reduced by essentially compressing the data before it is fed through the main network.

Conclusion

last modified 8 august 2000