Analysis of Conductive Bridge



An original solution was to run a heat conducting bridge from the hot exhaust stack to the intake stack. The solution proposed that enough heat would conduct from the exhaust stack to the intake stack to melt any incoming snow passing through the intake stack. A schematic is shown in figure 2. After a detailed analysis of the system, it was determined that this system was not a valid solution to our problem. The following points confirm this decision:

We assumed our conductive bridge to be 10 cm in diameter. The bridge needs to span 40 cm. So the volume of the bridge would be:


 
 

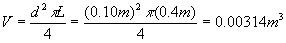
Using stainless steal with a density of 8000 kg/m3, the weight of the bar is 25 kg or 55 pounds.

25 kg of mass would be supported between two stacks that are made of not much more than sheet metal. Any sort of even small vibration would probably destroy both stacks (intake and exhaust)

Caterpillar has explicitly stated that they do not want to impose any addition diver obstructions on the operator. Even though the system would be behind the driver, it is very important that the operator have as much visibility as possible from all sides when operating heavy machinery.
 

The heat would be conducting across the bridge through a crosswind. This crosswind would impose convective losses. Also, the intake stack is very prone to convective losses once the heat does get there because it is not insulated.

Even if the conductive bridge was assumed to be perfectly insulated, this system may not be able to provide enough heat to melt all of the incoming snow:

Thermal conductivity of stainless steal: 15 W/m*K

Heat of sublimation of water/ice: 333500 J/kg

Mass flow rate of intake air: 600 ft3/min = 0.283 m3/sec

Approximate density of snow in intake air: 0.01 kg/m3

Energy needed to melt snow = (333500 J/kg)( 0.01 kg/m3)( 0.283 m3/sec) = 944 W

Assume:


 

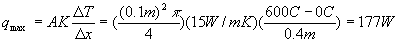
The maximum heat that our conductive bridge could provide under ideal steady-state and no heat loss conditions is 177W. But if the snow comes in with a density of 0.01 kg/m3, then it would need 944 W of heat to melt the snow. Clearly, this bridge could not provide the needed heat.

The conduction equation is governed by the diffusion equation, which is a slow process.

 

| BACK |